本篇文章轉載自微信公眾號“IT成長之家”，IT成長之家出了一個系列的課程，涉及數據分析、挖掘、預測等等方面的知識。如果大家感興趣的話可以點擊本文下邊原文鏈接到IT成長之家公眾號進行學習。

01? ?前言

線性回歸分析是一種很常見的數據分析方法。用于分析因變量是如何受到一個或多個自變量影響的。常用來分析或者預測某個產品的銷量與產品的價格、質量、市場活動等等因素之間的關系。

線性回歸根據自變量的多少，分為一元線性回歸和多元線性回歸。當然在實際工作生活中，我們往往都是面對著多元線性回歸。

02 案例介紹

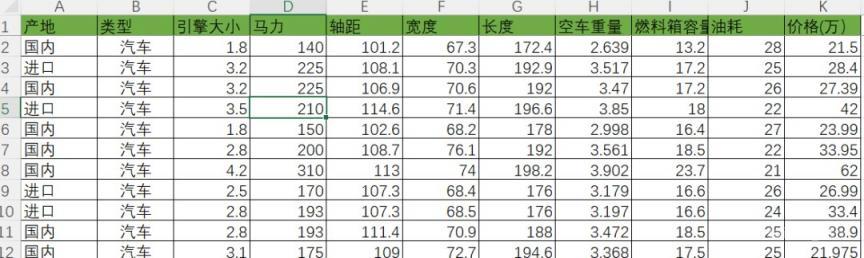
在本案例中，我們有這樣的一份數據。已知汽車的產地、類型、型號等等基本屬性（A-J列），同時也知道它的價格（K列）。

現在我們需要找出價格（因變量）與這些基本屬性（自變量）之間的關系，找出是否存在一個模型（方程），從而來判斷新生產的汽車，它對應的價格應該定價在哪比較合適。

03?操作分析

1）打開加載項：文件-選項-加載項-轉到，勾上“數據分析庫”，點擊確定。

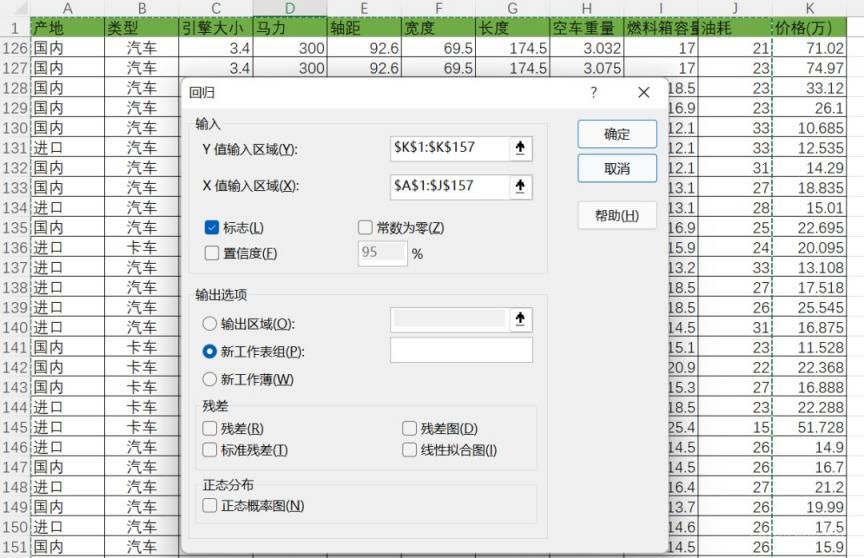
2）點擊Excel菜單欄 "數據"- "數據分析", 選擇“回歸”，Y值區域選擇K列范圍，X值區域選擇所有自變量因素。點擊確定。

（注意，在此模型中，我們需要先對“產地”，“類型”進行數值轉換，比如0，1代替）

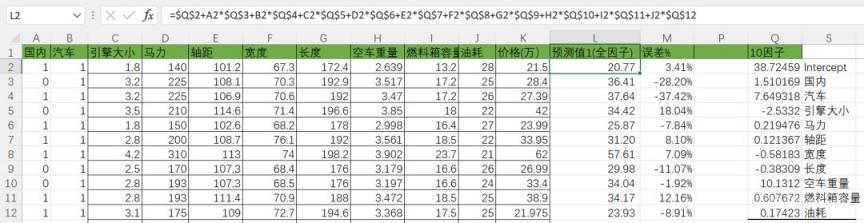
3）回歸方程建立之后，我們求出Ru，然后根據t-Stat(影響度)進行排序，去除影響度最低的因子，反復求出Ru值，直到最后一個因子。

4）求出10個Ru值，根據Ru值可以看到，最優的回歸方程是Ru值最大的，即10個因子。

5）因此我們的回歸方程即可出來（Y= 常量+a*x1+b*x2+....）

同時也可以求出誤差率，對預測值的誤差有個整體判斷。

04?回歸方程的解讀

回歸分析的計算結果一共包括三個模塊：

第一個模塊為回歸統計表，其中主要包含MultipleR、RSquare、AdjustedRSquare、標準誤差和觀測值。

MultipleR為復相關系數，也就是前面說的相關系數，用來衡量x和y之間的相關程度大小。R?Square為復測定系數R2，其用來說明自變量解釋因變量變差的程度，從而測量同因變量y的擬合效果。Adjusted?R?Square為調整后的復測定系數R2，標準誤差衡量擬合程度大小，值越小，說明擬合程度越好，觀測值指的是用于估計回歸方程數據的觀測值個數。

例如，從上面結果可以看出，MultipleR為0.900393，表明是有很強的正相關性；R Square為0.810708表明用自變量可解釋因變量變差的81.07%；AdjustedRSquare為0.797654，說明自變量能說明因變量的79.76%，因變量剩余的21%則由其他因素來解釋。

第二個模塊為方差分析表。其主要作用是通過假設檢驗中的F-檢驗來判斷回歸模型的回歸效果。

第三個模塊是回歸參數表。第一列表示截距；第二列表示對應模型的回歸系數，包括了截距和斜率，可以根據這個建立回歸模型；第三列為回歸系數的標準誤差，值越小，表明參數的精確度越高；第四列對應的是回歸系數/標準誤差，對于一元線性回歸，F值與t值都與相關系數R代表差不多的意思，但是，對于多元線性回歸，t檢驗是有必要的。第五列為各個回歸系數的P值，當P<0.05時，可以認為模型在α=0.05的水平上顯著，或置信度達到了95%。最后幾列為回歸系數置信區間的上限和下限。

05?最后

當然，預測是代表著有一定的不確定性。這些不確定性包括無法解釋的原因以及不能預測的波動性。因此預測不可避免的會產生誤差。

因此線性回歸預測方程實際是：

并且，建立線性回歸模型也必須滿足一定的條件：例如方差齊性，獨立性，正態分布等等。

好了，如果想查看本例使用的數據，請在微信公眾號“IT成長之家”后臺回復 "線性回歸"，將會自動發送本推文所用的EXCEL表，包括初始數據、數據處理及模型建立的全過程。下期再會！